Crne rupe
Fizičari vole paradokse. Možda je to neobično, ali svoje profesionalne živote provode tražeći situacije koje će naterati njihov pogled na svet da se uruši, jer iz ruševina može niknuti dublje razumevanje. Dobrim naučnicima nije cilj da se njihova uverenja potvrde kroz istraživanje, već žele da istraživanje generiše nova uverenja.
Brajan Koks i Džef Foršo, Crne rupe
Još u mladosti sam saznao da postoji objekat toliko masivan da ni svetlost ne može da ga napusti, nadam se da većina omladine takođe to zna (i danas i u Srbiji - mada nam novi događaji govore da nemamo da se čega stidimo). Stvari ni "Nauci" (odnosno za to stručnima) ipak nisu još najjasnije, a neko sa latentnim interesovanjima bi svakako trebalo da pročita knjigu gde sve to ima sistematizovano, ranija i ona novija saznanja. I jedna i druga su u velikoj meri spekulativna - to što svetlost ne može da napusti crnu rupu znači da ne može ni informacija, barem ne ona koja bi nam bila zanimljiva u realnom vremenu (zapravo poslednja poglavlja knjige posvećena su tome može li informacija načelno da napusti, odnoso "preživi" crnu rupu, na to ćemo se vratiti). Kako ne možemo imati signal, odnosno rezultat merenja, koji napušta crnu rupu, znači da ne možemo eksperimentisati, sve i da do takvog objekta jednom dođemo (jedna je u centru naše galaksije). Možda bi mogli ako neku mini napravimo...
Knjiga je zanimljivo napisana, ali ne povlađivanjem lakšem čitalačkom ukusu, što može da znači da će biti težih poglavlja, ne zbog stila izlaganja, nego zato što su teme takve. Barem se nadam da nisam nešto pogrešno razumeo, i da ništa bitno nije izostavljeno. Milan M. Ćirković (i njega sam nedavno čitao) odaje priznanje autorima baš na tom nepristajanju na "nauku za decu", plus na Penrouzovim dijagramima. Za ovo drugo ipak ne mislim da je ne znam kakva smelost, nisu ti dijagrami mnogo komplikovaniji od Fejnmanovih, koje je on sam opušteno koristio u svojoj knjizi QED (kvantna elektrodinamika). Brajan Koks mi je inače već poznat, iz knjiga i klipova, drugi autor nije.
Kratka povest crnih rupa je prvo poglavlje gde vidimo razvoj te ideje, koji seže još ranije od Ajnštajna (i Minkovskog). Tako je još Laplas tvrdio da u svemiru mogu postojati objekti koji su toliko veliki (on je računao da imaju gustinu Zemlje) da ih svetlost ne može napustiti, i takav objekat po njemu bi imao prečnik 250 puta veći od prečnika Sunca. Zaključak je da najveći objekti u svemiru mogu biti nevidljivi - apsolutno aktuelno i danas, samo bismo rekli najmasivniji. Meni je tu zanimljiv prvi korak u zaključivanju - da svetlost ima ograničenu brzinu. Jer, zašto svetlost ne bi dolazila trenutno, ideja da ipak ima neku brzinu (tada se još nije znalo za apsoluto ograničenje c - brzina svetlosti) mogla je doći od čestične teorije svetlosti, koja je delimično tačna i možemo je zahvaliti Njutnu. Određena brzina, topovskog đuleta recimo, može biti dovoljna ili ne da se pređe neko odstojanje, možda pobedi gravitacija, teoretski kad to znamo nije daleko zaključak da bi prevelika težina i za svetlost bila nepobediva.
Onda kreće stvar sa Penrouzovim dijagramima. Oni nam se prvo predstavljaju u običnom prostoru, sa svojim beskonačnostima u vremenu i prostoru. Postoje oblasti koje su kauzalno nepovezane, što proizilazi iz relativnosti. Međutim, može se sve to i šire posmatrati, jer da bismo reagovali na nešto, potrebno je da imamo informaciju, a ona realno može do nas putovati mnogo manjom brzinom od c. Evo šta sam napisao.
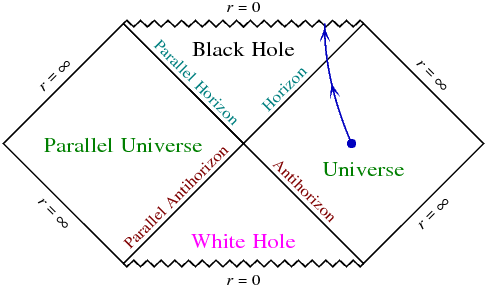
Popularna nauka tera na razmišljanje, naravno na čitaocu je da širi temu. Na slici je Penrouzov dijagram, koji predstavlja kako prostorvreme deluje. Možda je dovoljno objašnjenja da su bela područja levo i desno ona koja nisu, kako se kaže, kauzalno povezana - informacija ne stiže do njih i nazad, šta se tamo desi ne utiče ovde i vice versa (naravno, govori o događaju u prostoru I vremenu, aktere tog događaja možemo sresti kasnije)...
Primer je čekanje Božića 1974, rasprava je šta će se gledati na TV (ako je samo jedan, porodica nije u USA), baka prolije nešto preko grejalice, nastane kurcšlus i svejedno ne može ništa da se gleda... Šta se događa u stanu dve ulice dalje naravno da je nebitno za priču. To su te bele oblasti. Ali, čisto sa stanovišta brzine svetlosti, to je infinitezimalno. Čak u istoj sobi događaj u "bukvalno isto vreme", neko apsolutno, nije kauzalno povezan. Reč je o milionitim delićima sekunde.
No mi ipak imamo "light cone" u realnom životu, u smislu da nešto što je istovremeno ne utiče na događaj, prosto jer treba vreme da se prenesu informacije. Da je baka htela nekog da obavesti o događaju, zvala bi telefonom, pa ovaj dok se javi, čuje priču, zaključi šta da radi... tek tad može da reaguje. Sad sa smartfonima ne bi išlo mnogo brže, možda malo... Tek tad dva događaja deluju jedan na drugi, iz Ajnštajnovog ugla su "istovremeni".
Dakle granicu te kupe prošlih i budućih događaja koja je na liniji brzina prenosa infomacija + brzina obrade informacija. Da zanemarimo ovo drugo, poseban je račun koliko nekome treba da razume poruku i reaguje. Zanimljivo da udaljenosti na ovoj našoj planeti ne znače mnogo, informacije se prenose skoro trenutno, samo ih treba primiti. Časovna zona može imati nekog značaja, ljudi ponekad spavaju, mada ne svi u isto doba noći (ili dana).
Nekada su udaljenosti na planeti zapravo veoma imale uticaja. Uzmimo neki dan za početak američke revolucije, neki drugi događaj istog dana u centru Imperije, Londonu - naravno da je nezavisan, vest o revoluciji je putovala oko dve nedelje.
Subjektivno kupa može biti različito postavljena. Recimo ova tragedija u Novom Sadu - čuo sam u podne da je pao "deo fasade" i da ima povređenih, možda i mrtvih. Otišao kod zubarke, gde se samo čuje muzika, čim sam završio pustio veseli snimak sa Noći veštica. Tek pola sata kasnije video sam koliko ima mrtvih, pa da muzika baš i nema smisla. Valjda je pozitivno ne pratiti vesti svakog minuta...
Tako možemo videti kako su događaji relativni i pri brzinama mnogo manjim od relativističkih, što su one veće od c/4.
Upoznaćemo besmrtnike, entitete koji ne podležu starenju i nekim fizičkim tegobama, a van crne rupe stvarno i žive neograničeno. Stvari se komplikuju u prisustvu ogromne mase. Tada će ovi besmrtnici, obojeni različitim bojama, svaki sa svojim imenom i muzikom koju sluša, skoro svi pohrliti ka singularitetu - središtu crne rupe. Penrouzovi dijagrami će se ovde pokazati veoma korisnim. Videćemo kako će oni koju uđu to uraditi ne osetivši nikakvu promenu (i barem što se tiče gravitacije u nemogućnosti da utvrde da se nešto dogodilo), ako je crna rupa dovoljno masivna i statična. Neko izvan horizonta događaja videće nešto drugo - kako njegov prijatelj sve više usporava ka tom horizontu (crnoj rupi) a da ga nikada ne pređe, na njemu se zamrzava. Ovaj dualni pogled dobiće na značaju kasnije.
U crnoj rupi je poglavlje koje se time bavi. Kako imamo besmrtnike, oni neće patiti od špagetifikacije (o čemu ćemo videti kasnije), ali ipak imaju kraj vremena. Saznajemo da singularitet nije tačka u prostoru nego u vremenu i to sledi iz Penrouzovih dijagrama. Sve to je, iako iz dobro poznate teorije Ajnštajna (i ostalih koji su proučavali) spekulativno - rekosmo da nemamo merenja da nam potvrde. Zapravo sva objašnjenja vode tome da ih i ne možemo imati.
Ova knjiga se ne bavi nekim "fizičkim opisom" singulariteta, da li je to tačka bez dimenzija (a neograničene gustine) ili kvantna pena, što se izgleda i ne smatra bitnim s obzirom na slom prostorvremena ispod Plankove dužine. Zato ćemo dobiti opise koncepata u poglavlju Bele rupe i crvotočine - što takođe sledi iz Penrouzovih dijagrama. Moguće je tako zamisliti objekat iz kojeg nešto samo izlazi, opozit crnoj rupi, mada ne znam za empirijsku potvrdu. Možda je u drugom svemiru. Crvotočina bi upravo vodila u drugi svemir, ili bila prečica za putovanje kroz ovaj, mada to ne može biti jer je zatvara "materija" (valjda masa?). Spekulativno je da li se može napraviti crvotočina koja bi bila prohodna. Za neke praktične primene (budućnosti), crvotočina ili wormhole možda je ipak gubljenje vremena.
Prostorveme, preko Penrouzovih dijagrama jedna je od dve velike teme ove knjige, a druga je termodinamika crnih rupa, ali pre toga ćemo se upoznati sa Kerovim crnim rupama, onim koje rotiraju, mogućim izlascima iz njih i golim singularitetom, koji bi vas mogao izbaciti bilo gde, i u prošlosti. Naravno, nešto što naučnici ne vole. Tu je naravno i ono što se zaista dešava u crnoj rupi - kako bi prošao čovek a ne besmrtnik. Da li bi bio spržen pri ulasku u crnu rupu ili preživeo špagetifikaciju koja nastaje iz veoma nejadnakog delovanja gravitacione sile, čak i na pete i glavu istog čoveka.
Najzad dolazimo do termodinamike (i entropije) crne rupe, nečega što je neizostavno vezano za Hokinga - velikana ove oblasti koji je i sam pravio velike greške i priznavao ih. Termodinamika crne rupe je nešto što baš i ne očekujemo, jer crna rupa je veoma prost objekat kojeg određuje tek nekoliko veličina - masa (preko nje i površina horizonta), elektromagnetno i obrtni momenat (druge dve veličine, ako postoje). Ali šta se dešava sa objektima koji upadnu u crnu rupu? Gde "nestaju" informacije? Upravo je to vezano za entropiju, najveću moguću, koja je data formulom toliko značajnom da se nalazi na Hokingovoj nadgrobnoj ploči u Vestminsterskoj opatiji.
Ovde se uponzajemo sa konceptom po kojem informacije u crnoj rupi mogu biti u potpunosti kodirane na površini (meni to nije sporni zaključak, pošto mi za bilo koje neprozirno telo, a crna rupa to svakako jeste, bilo šta možemo saznati samo na osnovu onoga što spolja vidimo). Ako bismo crnu rupu popločali bitovima na horizontu događaja, dobili bismo njenu informacionu vrednosti, takođe koliko se informacija (maksimalno?) može uskladištiti u odgovarajućoj masi. Ipak, ostaje prvi od dva velika problema - sve su ovo zaključci po analogiji, samo objekti sa temperaturom mogu imati termodinamiku, a to su oni koji nešto zrače, crna rupa po definiciji ne može da zrači. Upravo je to demantovao Hoking, primenom kvantne mehanike dobijamo ono što se zove Hokingovo zračenje.
Drugi od dva velika problema vezan je za "rat crnih rupa" koji je Hoking vodio i izgubio sa Saskindom (u ovoj knjizi vidimo njegov veliki talenat za zanimljive naslove naučnih knjiga i radova, ja ga pamtim po citiranju Šerloka Holmsa: kad odbacimo sve što je nemoguće, dobijamo istinu ma koliko neverovatna ona bila). Dakle, po Hokingu crna rupa će na kraju (za recimo deset na stoti godina) da ispari, ali mi nećemo ni u principu moći da dekodiramo informacije iz nje, tj. da ih povežemo sa nekim davnim stanjem pre ulaska u crnu rupu. Ovde imamo dosta objašnjavanja i malo čudnih tipa ako sakupimo sav pepeo nekog koje izgoreo dok je upadao u crnu rupu (pogled spolja), nećemo moći da upadnemo za njim i taj mu pepeo pokažemo (pogled iznutra), što brani neku logičku stabilnost. No već je poznato da je Hoking tu bitku (i opkladu) izgubio, informacije su očuvane i u crnoj rupi.
Ova pomenuta neverovatna istina je upravo Holografski princip, koji može da važi i u za svemir koji je naš, u kojem slučaju smo mi na dnu crne rupe, program kvantnog kompjutera. To je, naravno, spekulativna teorija, jedno od mnogih objašnjenja realnosti (kosmologije? ali kako objašnjava nastanak svemira?), pa kako druga imaju paradokse, možda baš ovo važi. Uz značaj informacije, dualnost je moj pogled na svet, tu je i dobro nam poznat princip kako gore tako dole. Poglavlja tako postaju sve više spekulativna, uz Maldaseninu teoriju koja je sasvim naučna, ali izgleda da nije bilo dovoljno kako je ovde prikazano da bi, makar meni, bilo sasvim jasno. Ali ako ću po sebi, priznajem da sam se dotle već pomalo umorio...
Poglavlja kao što je Zvuk tapšanja jednom rukom (što je inače iz zen-koana) svakako nam otvaraju nov pogled na ceo svet, dakle izvan crnih rupa, koje su same po sebi zanimljive. Razumljivo je da će se završiti citatom Van Goga: "Budite svesni zvezda i beskraja na nebeskim visinama. onda život izgleda gotovo kao ćarolija."
Ivan Vukadinović




Коментари
Постави коментар