Негативни бројеви не постоје?

Овде проблем шта је писац хтео рећи креће од самог наслова. Јер, шта значи уопште постојање? Да не идемо дубоко у филозофију, ограничићемо "област постојања" на појмове који имају представе. То не значи да други појмови не постоје, већ да постоје на... другачији начин. Али шта је број?! Овде се неће улазити у различита схватања по којима су бројеви својства објеката или класе којима додељујемо објекте, исл. Бавићемо се, дакле, постојањем представе нечега што је избројано или измерено негативним бројевима. Уочимо и знак питања, који нам додатно показује како се овде не доказује изричито непостојање скупа негтивних бројева.

Нисам ја први који о оваквим стварима размишља. Швајцарски легендарни математичар Ојлер имао је нелагоду поводом негативних бројева, па чак чудне идеје да су негативни бројеви већи од позитивних. Нешто у необавезном тону можете видети овде. Иначе, у једној дискусији о постојању и непостојању питах човека да представи минус пет јабука. Саговорник, у покушају духовитости, рече "Појели их атеисти". Тиме "постиже" два циља - кеца мрске му атеисте, и друго - брани своје виђење религије. Но, оно прво би се добило и на мој начин - ако доводимо у сумњу такве елементе "материјалног света" око којих се обично не сумња, релативизујемо само постојање, па што Бог онда не би постојао, на неки начин. Но међутим, ако је то постојање "релативно", односно не постоји представа Бога око које бисмо се лако сложили, онда све догме падају у воду, религије су различите, а не боље ни горе, па ни "слатко православље" није боље од шаманизма. Може се једино причати о логичкој конзистентности и етичко-историјским последицама различитих вера...

Иако не волим претерано оне модерне холистичко-позитивне форе, заправо ту фразеологију, слажем се да за космос не постоји НЕ. Уверила ме је психолошкиња у фирми која рече - ајд замислите да не радите нешто. Немогуће. Заправо то што не (треба да) радимо ће нас све више прогањати. На сличан начин немање нечега нема независну представу. 

У даљем тексту помоћи ће школски уџбеник логике. Можда је смешно да овакве ствари дефинишемо, али што не бисмо видели... Бројање је методички поступак којим се утврђује број чланова или елемената неког скупа или класе. Мерење је методички поступак којим се  уз помоћ неког прибора утврђује бројчана вредност неког екстензивног својства. Не постоји скуп чији је број чланова негативан, нити се може измерити апсолутно негативно својство неког објекта. 

Постојали као целобројни или реални бројеви, негативно постоје само кроз међусобни однос избројаног или измереног, или по конвенцији. Као такви јесу невероватно корисни људима. Погледајмо сад на које све начине негативни бројеви ипак постоје.

1. Као последица нечега у прошлости. Видиш две јабуке, а треба да их је седам. Дакле, то су оних пет које су појели атеисти. Или можда ипак мишеви, атеисти једу сендвиче с мајонезом. Ми и даље немамо независну представу тих пет које недостају. 

2. Нешто нам недостаје па планирамо у будућности, или смо већ позајмили па смо дужни. Дакле, хоћемо да поједемо седам јабука, а имамо само две. Међутим, ни прошлост ни будућност не постоје, само садашњост (мада и она некако... чудно)

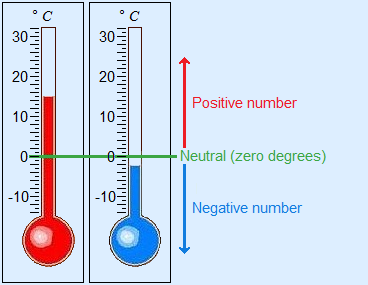
3. Реални негативни бројеви постоје по конвенцији. Тако је -10 целзијуса, нешто око 10 фаренхајта. Међутим ни једна ни друга скала није "права", а ни научно практична. Можда можемо колоквијално рећи да је 100 фаренхајта дупло топлије од 50, али научно или инжињерски, то нема никаквог смисла.

4. Негативни бројеви (обично реални) постоје кроз поларитет. Овде је такође једна конвенција - шта је плус а шта минус, док је сама "супротност" реално постојећа. Пример би било наелектрисање. Занимљиво је да својство по којем "минус пута плус даје минус"... односно, супротности се привлаче, истозначности одбијају постоју како у математици, тако и у "реалном свету". Мада су сад истосмерни некако модерни... Ојлер је такође о овоме размишљао. Занимљиво да "негативно" у овом смеру не мора бити тако негативно (лоше у свакодневном значењу). Негативно значи привлачење, негативна јонизација је добра...

5. Негативни бројеви постоје алгебарски. Неопходни су већ за решавање једноставних једначина. Код неких комплекснијих имамо комплексне бројеве, о чијем се "постојању" (путем представе) може такође свашта рећи, а они постоје као решење само у негативно-позитивном пару.

Погледајмо сада постојања неких других бројева. Као резултати бројења и мерења постоје позитивни цели (природни) и реални бројеви. Рационални бројеви постоје као однос два цела, и тако се увек могу једноставно изразити, мада је децимална нотација практичнија. Реалан број би се могао изразити као однос појава у природи, π је можда једноставан за разумевање као однос полупречника и кружнице, али је е нешто компликованији. Трансецедентан број се не може изразити као решење алгебарске једначине са коефицијантима који су рационални бројеви (разломци целих бројева). Може кроз развој где се тежи бесконачности, али...

Нула је... занимљив проблем. У суштини непостојање не постоји. Међутим, занимљива је културолошка разлика. Грци су игнорисали нулу, ако су за њу и знали. За Индусе она је можда највише постојећа. А за западну (фаустовску) науку нула је као сингуларитет велика непријатност. То видимо у данашњој физици, космологији... А што се тиче поменуте температуре, реално постоји само келвинова скала, док апсолутна нула према истој не може нигде у Природи наћи, нити се може измерити. Како згодно што су Њутн и Лајбниц дошли до инфинитезималног рачуна, мада то није решило све проблеме. А имагинарни и комплексни бројеви? Можда други пут, за сад је доста...

Иван Вукадиновић